2. 超平面和半空间

1. 超平面(hyperplane)

形如$\{x \mid a^Tx=b \}(a \ne 0)$的就是超平面

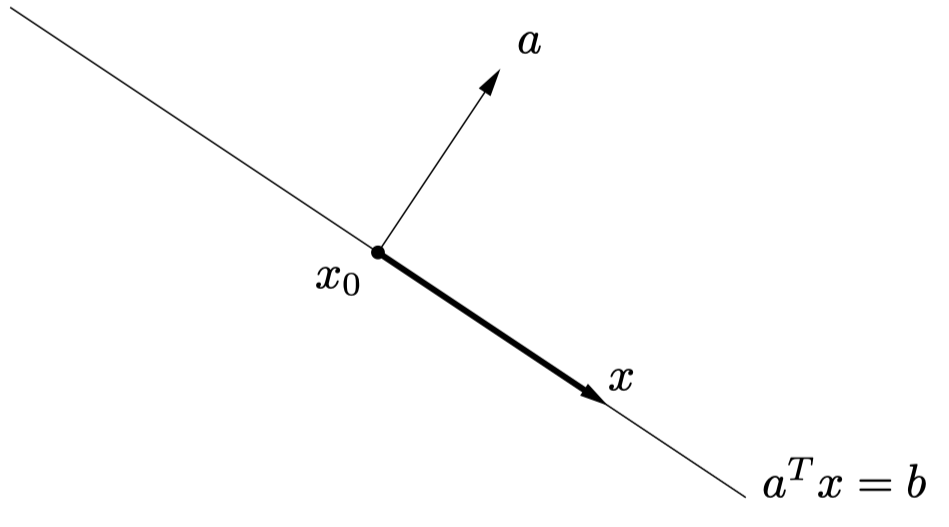
可以看成是一系列点的集合，这些点与向量$a$的内积为一个固定的常数。而$b$则是该超平面相对于原点的偏移量，原定义可以写作

$$\{ x \mid a^T(x-x_0)=0 \}$$

其中$x_0$为超平面上一点。

2. 半空间(halfspace)

超平面可以把$R^n$分割为两个半空间，形如$\{x \mid a^Tx \le b \}(a \ne 0)$的就是半空间

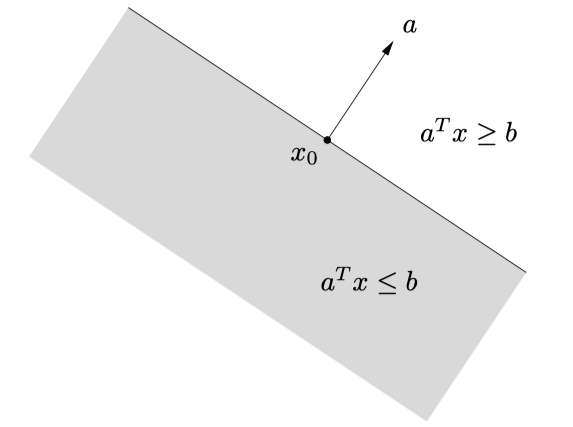
用定义可证，半空间也是一个凸集（[[1. 仿射集-凸集-凸锥#凸集 convex set]]）

3. 子空间(subspace)

要区分子空间和半空间。
所谓子空间，或者空间，即存在以下性质的点集合：对于$x_1, x_2 \in V$，有

$$\alpha x_1 + \beta x_2 \in V, \quad \alpha,\beta \in R$$